Geometric morphometrics

Morphometrics is the statistical analysis of shape. It is a set of techniques which are widely used in biological sciences to characterize, and quantitatively study, shapes of biological interest.

Geometric morphometrics is a younger area of morphometrics and it comprises a set of techniques which, apart from allowing the statistical analysis of shape (as in "traditional morphometrics"), retain geometric properties of objects throughout the analysis.

I am extremely interested both in using geometric morphometrics as a tool to answer biological questions and in exploring geometric morphometric methods themselves.

Up until now, I mainly worked with geometric morphometrics to study intraspecific variation in body shape and trophic structures (pharyngeal jaws) in various fish species.

A few basic info on geometric morphometrics

When studying a biological shape, such as fish body shape, with traditional morphometrics we could take a series of linear measurements between couple of points, such as standard length (SL). From the moment we take these measurements onward, we loose all the geometric properties of the original shape and we have only a series of numbers representing distances.

When using geometric morphometrics, instead, we keep the geometric information throughout the analysis. For instance, in the case of landmark-based geometric morphometrics (which is the most widely used "version" of geometric morphometrics), we acquire coordinates of points of the shape we want to analyze and carry out a series of statistical analyses on them. Given that we retained geometric properties throughout the analysis, at the end of the analyses we can visualize results as shapes, deformations of the original shapes or deformation grids.

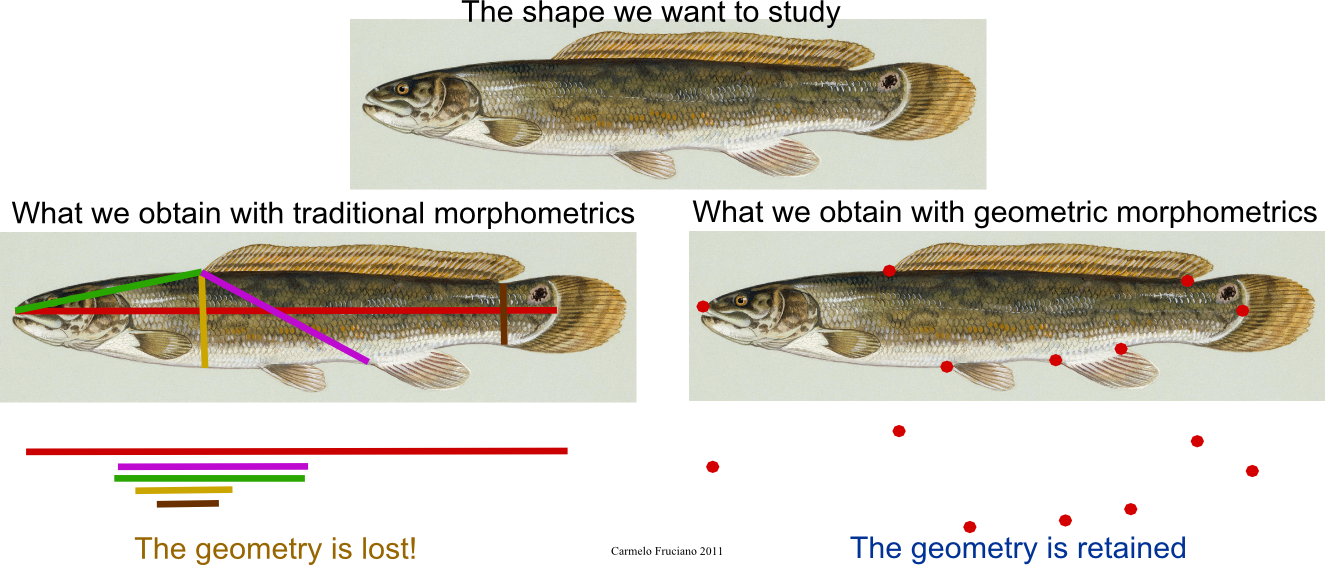
When using traditional morphometrics, we obtain a set of linear measurements and we loose geometric information. When we use geometric morphometrics, the geometric information is preserved

There are numerous other advantages in using geometric morphometrics versus traditional morphometrics, such as the lack, in geometric methods, of the redundancy of information present in traditional measurements; there is a wide literature on the advantages of geometric morphometrics.

A typical workflow for landmark-based geometric morphometrics is the following:

Obtain coordinates of landmarks (homologous points)
Obtain centroid size (which is a measure of size independent of shape which can be used in following analyses)
Carry out a Procustes superimposition (which optimally superimposes configurations of points by removing the effects of translation, rotation and scale)
Optionally (but often done for its advantages), carry out a principal component analysis (PCA) on the configuration of points obtained from the Procustes superimposition obtaining PC scores for each configuration of points (also called “relative warp scores”)
Analyze the PCA scores with statistical methods to answer biological questions (for instance, using discriminant analysis to compare a priori-defined groups or performing a multivariate regression of the PCA scores on centroid size to study allometric variation in shape)
Depict results of the analyses as shapes, deformed shapes or deformation grids

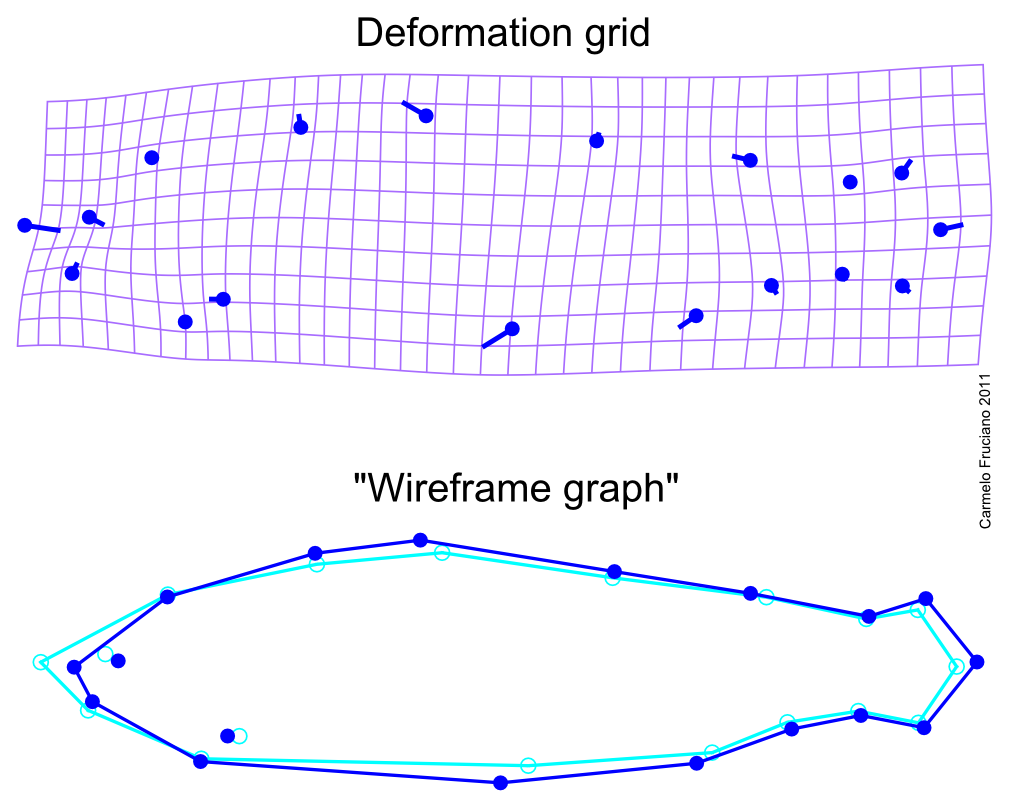
Two possible ways of displaying the results of a geometric morphometric analysis: the deformation grid and the wireframe graph

While landmark-based geometric morphometrics is probably the most used “version” of geometric morphometrics, there are many other methods that go under the “umbrella category” of “geometric morphometrics”. Among them, some of the most common are methods that analyze outlines by fitting mathematical functions to the coordinates of points of the outline (as in the case elliptic Fourier analysis) or by using points (called “semilandmarks”) that are not homologous but retain positional correspondence in a framework similar to the one provided by landmark-based geometric morphometrics.

This page is not intended to give a comprehensive treatment of the topic of geometric morphometrics but mainly to give a few basic info that help understand why I am so excited about geometric morphometrics.
For those interested, a simple literature search on Google Scholar will return many interesting papers (and books) that deal with geometric morphometric techniques more in detail than it is appropriate to do here.